Cloud cover
Total cloud cover, or total cloud amount, is one of the most common variables to characterize
cloud fields. According to the
[Observer's Handbook, 1982],
cloud cover is defined as
the fraction of the celestial dome covered by clouds. Some care has to be taken when referring
to cloud cover because especially for theoretical considerations, the quantity of interest is
usually the horizontal area covered by clouds rather than the fraction of the celestial dome.
Both quantitities are related but not neccessarily equal. For this reason, we use the term
skycover when referring to a ground-based observation of cloud cover,
and earthview for the horizontal coverage, as it would for example be reported
by a nadir-viewing satellite. The relationship between both has been investigated e.g. by
Lund [1965] or
Henderson-Sellers and McGuffie [1990].
Two fundamentally different cloud geometries were used here to investigate the relationship
between skycover and earthview: first, clouds were assumed
to be cuboids with square bases, arranged on a periodic square grid.
Second, clouds were generated using a cellular automaton as described by
Nagel and Raschke [1992] and applied
by Macke et al. [1997].
The following graph shows a cloud generated by the algorithm of
Nagel and Raschke [1992].
Each cell of the three-dimensional
field is completely described by three boolean variables: upwind, humidity, and cloudiness.
Each value can either be true or false. The evolution starts with a random humidity distribution,
and a one-pixel cloud seed in the center of the field. As the field evolves in time,
new values are assigned to each cell depending on its present state and on the state of the neighbouring cells.
Assigning a constant extinction coffecient to each cloudy cell, the optical properties of the
cloud field are calculated. The cloud field shown in the following graph is an array of 50 x 50 x 25
cells. Periodic boudary conditions are assumed in the horizontal directions, while in the
vertical direction, the evolution stops at the layer boundaries
(corresponding to dry layers above and below the cloud). Note that the brightness of the optical depth
images changes continuously because it is normalized to the maximum optical depth separately for each
image of the animation (otherwise, the images would be too dark in the beginning of the cloud formation).
|
Cloud optical depth |
|
Cloudy / not cloudy |
| Top view |

|
y |

|
|
x |
|
x |
| Side view |

|
z |
|
|
x |
|
|
A MonteCarlo model, developed for 3D radiative transfer calculations,
provides a convenient way to directly calculate skycover for given earthview and cloud geometry.
Photons were traced through an otherwise empty atmosphere with fully absorbing clouds.
Starting the photons from random locations at the surface, the area average of the
conversion factor is calculated. The next graph shows the relationship between earthview and
skycover for 12 cloud types which differ by their cloud bottom and vertical extension.
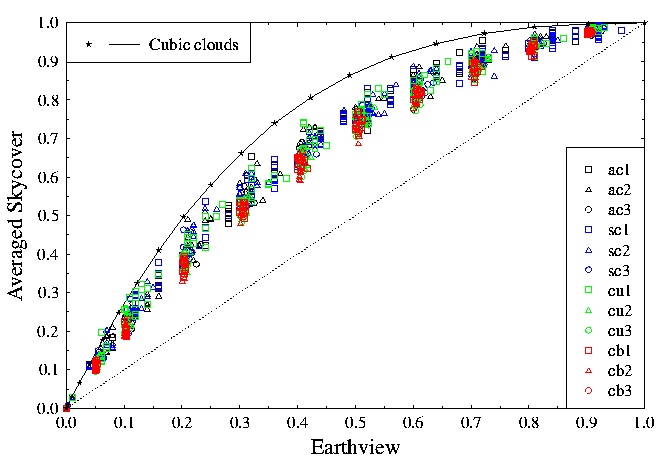
Although conceptually different, both cloud geometries lead to approximately the same result:
skycover, as observed from the Earth's surface, is systematically larger than earthview. This
is easily explained by the fact that the earthview is only the horizontal projection of the
clouds while both, cloud bases and cloud sides contribute to the skycover. This systematic
difference has serious consequences for the interpretation of ground-based observations
because model calculations usually are based on the earthview while from the surface only
skycover is available.
References
- 1
-
Henderson-Sellers, A. and K. McGuffie.
Are cloud amounts estimated from
satellite sensor and conventional surface-based observations related? Int. J. Remote Sensing, 11, 543-550, 1990.
- 2
-
Lund, I.
Estimating the probability of clear lines-of-sight from sunshine and
cloud cover observations. Journal of Applied Meteorology, 4,
714-722, 1965.
- 3
-
Macke, A., J. Mueller, K. Nagel, and R. Stuhlmann.
A cellular automaton model
for cloud formation: radiative properties. In IRS '96: Current problems
in atmospheric radiation, edited by W. Smith and K. Stamnes, Proceedings
of the International Radiation Symposium, Fairbanks, Alaska, 19-24 August
1996, pp. 234-237, A. Deepak Publishing, 1997.
- 4
-
Nagel, K. and E. Raschke.
Self-organizing criticality in cloud formation?
Physica A, 182, 519-531, 1992.
- 5
-
Observer's Handbook, ISBN 0114003297, Meteorological Office (HMSO), UK,
1982.






