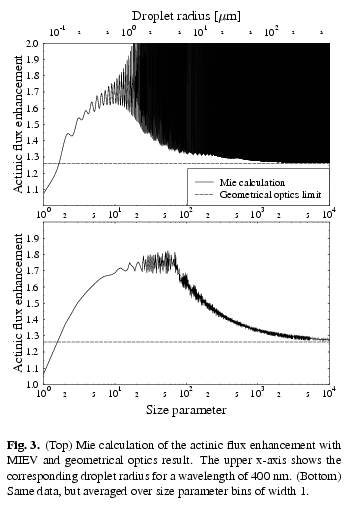

|
In a recent publication, [Mayer and Madronich, 2004] studied the actinic flux and photolysis in water droplets, using Mie calculations and geometrical optics. Photolysis of water-soluble components inside cloud droplets by ultraviolet/visible radiation may play an important role in atmospheric chemistry. Two earlier studies have suggested that the actinic flux and hence the photolysis frequency within spherical droplets is enhanced relative to that in the surrounding air, but have given different values for this enhancement. Here, we reconcile these discrepancies by noting slight errors in both studies that, when corrected, lead to consistent results. Madronich (1987) examined the geometric (large droplet) limit and concluded that refraction leads to an enhancement factor, averaged over all incident directions, of 1.56. However, the physically relevant quantity is the enhancement of the average actinic flux (rather than the average enhancement factor) which we show here to be 1.26 in the geometric limit. Ruggaber et al. (1997) used Mie theory to derive energy density enhancements slightly larger than 2 for typical droplet sizes, and applied these directly to the calculation of photolysis rates. However, the physically relevant quantity is the actinic flux (rather than the energy density) which is obtained by dividing the energy density by the refractive index of water, 1.33. Thus, the Mie-predicted enhancement for typical cloud droplet sizes is in the range 1.5, only coincidentally in agreement with the value originally given by Madronich. We also investigated the influence of resonances in the actinic flux enhancement. These narrow spikes which are resolved only by very high resolution calculations are orders of magnitude higher than the intermediate values but contribute only little to the actinic flux enhancement when averaged over droplet size distributions. Finally, a table is provided which may be used to obtain the actinic flux enhancement for the photolysis of any dissolved species. |